五轴机床误差建模与补偿解析新算法
全球化的竞争迫使生产企业越来越重视产品的加工效率和精度,产品精度很大程度上由机床的精度所决定。五轴数控机床能实现对复杂异型曲面零件进行高速、高效、高精度加工,广泛地运用在汽车、军工、能源等行业,近年来越来越倍受机械加工行业的重视。五轴数控机床受几何误差、热变形误差、动态误差等各种因素的影响,其加工精度往往很难满足实际生产需求。通过更换高精度传动部件和伺服控制系统来提高机床精度易受技术和生产成本等瓶颈的限制,因此对机床进行误差补偿已成为提高加工精度的一种有效方法。机床的误差主要有空间运动学误差、热变形误差、动力学误差以及运动控制与控制算法误差等,尤其是机床在加工过程中还存在热变形误差和承载变形误差,并且这类误差存在非稳定性和时序性,且分布较为复杂,因此,实现高精度误差补偿的关键技术是需要精确地建立数控机床综合误差的计算模型。目前,数控机床误差的理论建模技术主要有几何建模法、齐次误差矩阵法等几种。SheChenhua提出了一种通用型五轴机床误差补偿后处理模型,并有效地提高了补偿精度。文献和文献中采用多体理论对五轴机床的几何误差和热误差进行了简化与建模分析。Bohez 等提出了一种分离低阶误差分量的识别方法。尽管上述研究都取得了一定成果,但这些方法都存在着鲁棒性差、数学表达式冗余复杂、误差分量不确定、补偿精度差等问题,并没有从根本上解决机床误差建模和机床误差补偿的问题。作者以五轴机床CGM4000 为研究对象,基于多体动力学建立了误差综合补偿模型,尤其针对机床热误差,提出了5 点测量法和6 点测量法分别对主轴、进给轴进行热误差辨识。针对机床误差的不稳定性,不完整性等“贫信息”特性,提出了变权系数灰色模型( variable weight GM( 1,n) ,简称VW - GM( 1,n) ) 拟合热误差值,建立机床热误差预测模型。基于上述算法开发了易于数控系统自动解算的误差补偿单元,并通过试切加工验证了该补偿算法的有效性。
3)Z 轴( 低序体4) 相对Y 轴( 低序体3) 的综合误差变换矩阵T34 为:
4)A 轴( 低序体5) 固连在Z 轴( 低序体4) 上,综合误差变换矩阵为T45 为:
式中: A12=-εzAcos α+εzA·sinα; A13 = εzA·sinα+εyA·cosα; A22= cosα-εxA·sin α; A23-sinα-εxA·cosα; A32= εxA·cos α + sinα; A33 =- εxA·sinα +cosα ; 其中,摆头A 相对与Z 轴转动α。
式中,L 为刀具长度。
1 基于多体系统机床误差建模
1.1 五轴机床运动拓扑结构
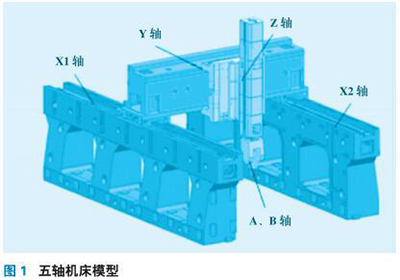
多体系统是指由多个刚体或柔体通过一定的约束形式连结而成的复杂机械系统。五轴数控机床分别由床身、工作台、横梁、立柱、进给单元、主轴单元等部件构成,各个运动部件都可简化为刚体或柔体子系统,运用低序体阵列对各子系统间的连接拓扑结构进行数字化描述。以CGM4000 型五轴机床作为研究对象,该机床为1 台标准类型的TTTRR(3 个平移轴T、2 个旋转轴R) 型五轴机床,结构如图1 所示。
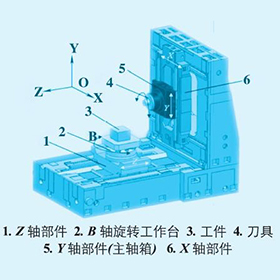
机床运动学模型是建立刀具坐标系相对于工件坐标系的运动关系,通常以各坐标轴在回零状态或对刀状态下的初始位置为起点,分析各运动刚体在运动过程中所引起的综合性误差。机床各运动刚体之间是刚性连接,每个运动刚体的运动学坐标关系都可以用一个4 × 4 的转置矩阵表示。在理想情况下,笛卡尔机床坐标系中X、Y、Z 轴之间两两相互垂直,回转轴A、B( 双摆头) 分别绕x、y 方向旋转,并与Z 轴固连,主轴S 固联在B 轴上。通过多体动力学理论对机床进行运动学拓扑分析,可以得到如图2 所示的低序体阵列拓扑结构图,其中机床主要部件分成9 个典型体单元。在机床床身上建立固定参考坐标系,确立机床运动副之间的相对位姿关系,建立起机床运动学约束方程。为了求解该型机床的运动学方程,建立两组运动学约束链,一组是刀具运动学约束链,另一组是工件运动学约束链。在床身( 低序体0) 上建立参考坐标系0; 工件( 低序体1) 上建立坐标系1; X 轴( 低序体2) 上建立坐标系2; Y 轴( 低序体3) 上建立坐标系3; Z 轴( 低序体4) 上建立坐标系4; A 轴( 低序体5) 上建立坐标系5; B 轴( 低序体6) 上建立坐标系6; 主轴S( 低序体7) 上建立坐标系7; 刀具t( 低序体8) 建立坐标系8; 通过低序体0、1、2、3、4、5、6、7、8 建立了机床运动学拓扑约束链。
1. 2 误差分量解析
文中该型数控机床的X1 轴和X2 轴由于误差特性相同,故统称为X 轴的误差,根据机床结构和热误差特性分析,该型五轴机床共有59 个误差分量,其中37 个几何误差分量,22 个热误差分量,具体描述如下:
1) 在空间坐标系中,3个运动平移轴有6 个误差分量,双摆头A、B 轴各有6 个误差分量,共30 个误差分量。各轴的误差分量分别为: 在x、y、z 方向的3 个线性平移误差δij( i = x,y,z; j = X,Y,Z,A,B)和绕X、Y、Z 坐标轴的3 个角位移误差分量εij( i =x,y,z; j = X,Y,Z,A,B) ,其中,i 为误差的方向,j 为运动轴名称。δxX、δy X、δz X为X 轴的坐标系原点分别在x、y、z 方向的平移误差,εxX、εyX、εzX为X 轴的坐标系原点分别在x、y、z 方向的回转误差。
2) 在空间坐标系中,X、Y、Z 轴间的相互垂直度误差Sxy、Sxz、Syz共3 个误差分量。
3) 在空间坐标系中,A、B 回转轴误差为: A 轴与xy平面及yz平面的平行度误差SAxy、SAyz; B 轴与xz平面及yz平面的平行度误差SBxz、SByz共4 个误差分量。
4) 每一个运动轴( X、Y、Z、A、B) 在x、y、z 方向各有3 个热变形误差,共有15 个热误差Δδij( t) ( i= x,y,z; j = X,Y,Z、A,B) ,其中: i 为误差的方向,j为运动轴名称,如: ΔδxX( t) 、ΔδyX( t) 、ΔδzX( t) 为X轴的坐标系原点分别在x、y、z 方向的热变形误差,主轴S 在x、y 方向有2 个角位移误差εxS、εyS; 主轴S在x、y、z 方向有3 个热变形误差ΔSj( t) ( j = x,y,z) ,其中,j 为产生误差方向,另外主轴还存在x、y方向上热倾斜误差,分别为: ΔεxS( t) 、ΔεyS( t) ,共22 个误差分量。
1. 3 建模过程
1)X 轴( 低序体2) 固连在床身上( 低序体0) ,综合误差变换矩阵T02 为:

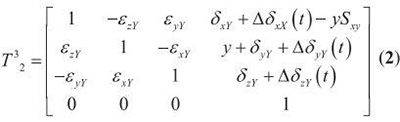
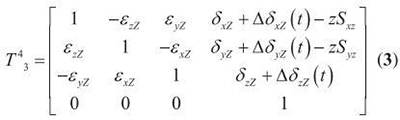
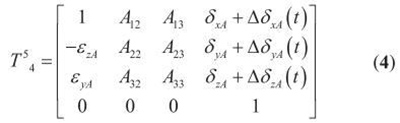
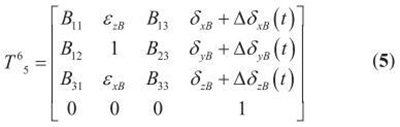
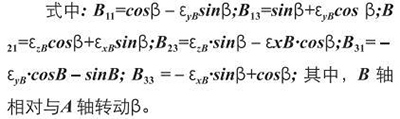
6)主轴S( 低序体7) 相对于B 轴( 低序体6) 的综合误差变换矩阵T76 为:
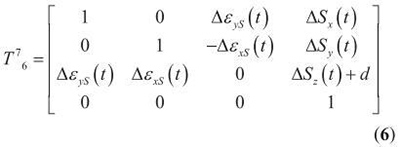

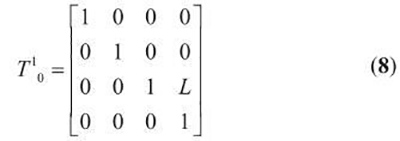
式中,a、b 为工件坐标系相对基坐标系的位置。
在理想状况下,刀具坐标系T 与工件坐标系W是重合的,但实际加工中由于机床的各种误差因素而导致两者之间并不重合。为了重新使其重合,必须对机床综合误差进行补偿,令WET表示刀具中心点实际位置和理论加工点的矢量偏差( 即误差矩阵) ,则Tr,t = WETW忽略所有2 阶及2 阶以上的高阶误差项,故综合误差模型化简为:


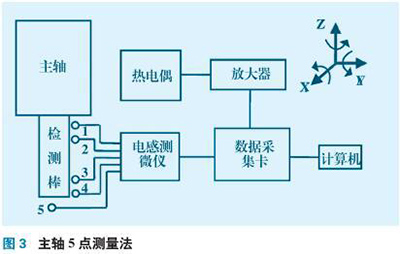
通过第1.3 节分析,基于小误差假设,机床综合误差E0可以看成机床几何误差E1和热误差E2的线性叠加,即E0= E1+E2。几何误差分量可以采用15 线、22 线等方法辨识出,已被广泛引用,故本节不再说明。本节主要针对热误差展开研究,提出了测量主轴热误差的5 点测量法和测进给轴热误差的6 点测量法。测量系统包括: M10 激光干涉仪、EC10环境补偿单元、分光镜、反射镜、PC 机、电感测微仪和温度热电偶。根据文献,在机床主轴和X1 轴的热敏感点处出安装热电偶温度传感器和电感测微仪进行数据采集。如图3 所示,测量主轴在x、y、z 方向的热偏移误差和绕x、y 方向的热倾斜误差,其中1、3 为x 向测量点,2、4 为y 向为测量点,5为z 向为测量点。通过数据采集卡获取相应的热变形量σi( t) (i = 1,…,5) ,则: ΔSx( t) = (σ3-σ1) ; ΔSy( t) = (σ4-σ2) ;ΔSz( t) = -σ5; Δεxs( t) = ( σ3-σ1) l /l1; Δεys( t) =( σ4-σ2) l /l2; 其中,l1为1、3 测量点间的距离,l 2为2、4 测量点间的距离,l 为主轴长度。
3 误差补偿实验与分析
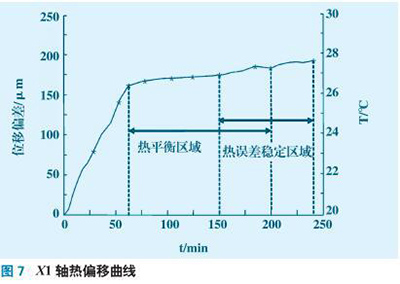
基于上述模型算法,为了验证该算法的有效性,以CGM4000为实验对象,该机床X、Y、Z轴行程为:4 000、2 500、600 mm,配置FIDIA 的双摆头,A 轴转动范围+90°~-110°、B 轴转动范围±360°。该型数控机床承重件采用了热对称结构设计,进给轴采用一端固定,另一端浮动的结构,有效地减小了由温升而引起的丝杠翘曲变形误差,并消除了丝杠反向间隙。进给丝杠选取THK 的空心滚珠丝杠,由于采用中空内冷方式,有效降低了滚珠丝杠的温升,最大限度的减少了滚珠丝杠副的热变形误差,从而保证了机床的高定位精度。数控系统采用SIMEMS840D,该系统具有良好的开放性,可将机床误差补偿算法集成到数控系统中去。考虑机床加工工况因素,反复优化补偿参数,通过数控系统内部的PMC 单元开发一种新型的五轴机床综合误差补偿系统。在机床加工过程中,若干个关键点的温度值和热误差值可通过热电偶温度传感器、电感测微仪等仪器来采集,将数据输入误差补偿模型中进行解算得到补偿值,补偿值反馈到机床CNC 系统,由CNC 系统驱动各轴电机控制器,完成实时补偿。基于上述条件以X1 轴为例进行实时综合误差补偿验证,其余进给轴验证方法相同,鉴于篇幅关系这里不再赘述。为了获取机床的热平衡区,以X1 轴为研究对象,机床开启循环冷却系统进行试切加工,以加工某型叶轮为例,工件毛坯材料0Cr18Ni9Ti,机床主轴转速为1200 r /min,进给速200 mm/min。X1轴位移偏差值和机床温度的关系如图7 所示,在20 ~26.3 ℃区间内,机床温度随时间上升,变化趋势陡峭,在26.3 ~27.2 ℃区间内,机床温升曲线随时间变化趋势平缓,此温度区间为机床的热平衡区域。另外在20 ~26. 8 ℃区间内,X1 轴热位移偏差随温度升高变化明显,而在26.8 ~27.8 ℃区间X1 轴热位移偏差量热位移偏差随温度升高变化趋势平缓,此温度区间为机床的热误差稳定区域,该区间与热平衡区间部分重合,在这段区间内机床的热误差处于一个有规律的稳态。实测X1 轴热误差偏移量如图8 所示。
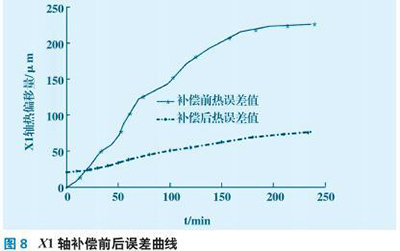
从图8 中可以看出,X1 各轴的热误差偏移量减慢,通过误差补偿算法,完成补偿后误差变化量在0 ~ 29 μm 之内。由此可见机床综合误差补偿系统是非常有效的,机床的精度有了显著的提高。另外,若因冷却系统发生故障,则会导致机床由于温升过高,数控系统报警而无法工作,此刻机床热误差处于无序状态,不在本文讨论范围之内。
4 结论
通过对五轴数控机床的误差分量进行了解析,综合各轴误差完成了误差补偿理论建模和实验分析,得到了如下结论。
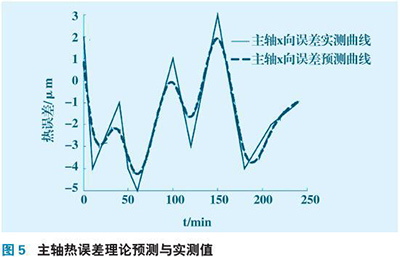
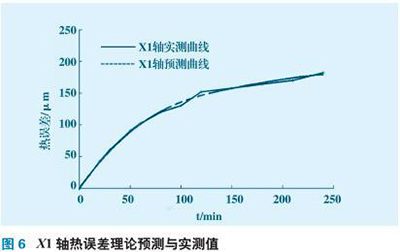
1) 利用多体运动学构建CGM4000 五轴机床综合误差模型,并对59 个误差分量进行相应的解析。综合机床各轴热误差产生的机理,提出了对主轴和进给轴热误差分量新的测量法: 5 点测量法和6 点测量法。大量实验证明理论预测辨识曲线与实验结果一致,主轴预测误差范围在0 ~ 2 μm 之间,进给轴预测误差范围在0 ~ 12 μm 之间。
2) 基于灰色系统理论表征离散点数据拟合出各轴热误差量曲线,建立了VM - GM( 1,n) 机床热误差预测模型,完成了五轴机床的非线性温度误差在线补偿模型。基于此模型大大提高了温度误差的预测精度,为误差补偿提供了补偿量预测值。
3) 通过修改机床数控系统的相关参数,基于数控系统PMC 控制单元,开发了一种实时的机床误差补偿系统。以X1 轴为例,实验表明当机床达到热平衡后,补偿前和补偿后,机床X1 轴热误差偏移量有了显著的降低,误差变化量在0 ~ 29 μm 之内,机床精度有很大提高。实现了采用软件算法补偿硬件误差。
上述结论表明作者所提出的五轴机床综合误差解析算法和误差补偿模型得到了实验验证,能有效提高机床的加工精度。考虑切削力作用下的机床综合误差建模与补偿将是下阶段的研究重点。
 销售热线:159 8941 5020
销售热线:159 8941 5020