数控机床运行激励实验模态分析
数控机床在工作状态下的结构动力学参数对加工效率和加工表面质量具有重要意义.机床在实际工作状态下的动态特性与其在静止状态下的动态特性不同,因此在机床静止条件下进行模态实验分析得到的结构模态参数不能准确反映机床结构的实际动态特性.并且,对于结构规模较大的数控机床,现有的激励设备也难以激励起结构的有效振动.由于机床是由众多零部件组成的复杂结构,又是在多变的动态条件下工作,通过理论建模的方法建立起能够精确模拟机床结构的动力学模型十分困难.同时还必须考虑各结合部间的动力学特性,理论建模的精度更难以满足实际需求.通过分析机床实际运动中振动响应可获得机床在工作状态下的动力学参数.但数控机床工作点的激励力难以测得.近来年,在桥梁和建筑上采用的工作模态分析方法,在传统的输入难以或无法实施的情况下,即可实现仅从输出信号中估计出模态参数.本文针对机床运行过程中的结构动态特性参数识别提出了机床运行激励的方法,通过响应数据进行机床的结构参数辨识,对运行过程中的机床结构进行在线模态分析.
1 运行激励方法
1.1 运行激励设计
图1是通过平面光栅测得的数控机床伺服轴在不同加减速常数作用下的加速度(Heidenhain公司的KGM182平面光栅,进给轴以10m/min进给200mm,通过位移数据差分得到伺服轴减速度),图中:a为加速度;t为持续时间。从试验结果可以看出:速度突变过程中,不同加减速度时间常数作用下,产生的加速度大小均不同,而产生的激励力则与速度改变过程中的加速度大小和持续时间有关。通过改变数控装置中的参数设置,可实现对激励幅值和频带宽度的有效调控。
1.2 运行激励试验
2 参数识别
ITD法通过对自由振动响应信号进行3次不同的延时重采样,得到矩阵
以得到的3个矩阵构造出结构的自由响应增广矩阵,将系统模态参数问题转化为求解系统特征值和特征向量问题。根据特征值与特征向量的函数关系,即可识别出结构的模态参数.
2.2 识别方法
规模较大的数控机床,其结构低频振动是影响加工质量和加工效率的主要因素;因此,确定待识别自由度数m=3,并以2m作为ITD法中识别模态数N的初始值,即N=6。不断提高N值,可得到一系列识别结果。但随着N值提高,识别结果中的伪模态也不断增加,因此N值不宜太大。
3 实验结果分析
3.2 识别结果分析
在数控机床伺服进给加减速过程中,由于工作台惯性引起的冲击激励通过丝杠轴承座传递到机床各个部分,引起机床整机结构的振动响应.对于冲击激励,脉冲宽度和脉冲形状是影响单个脉冲频谱特性的主要因素,脉冲愈尖,持续时间愈短,频谱的平直性愈好,如果力脉冲的频谱在感兴趣的频率范围内基本上是平直的,相当于给机床施加了一个宽带随机激励。
采用机床的运动部件变速运行可对机床结构进行运动激励,但直接采用数控G代码对机床进行控制,由于机床数控系统加减速控制、驱动系统控制规律以及被控对象的电气和机械惯性等影响因素,将使得运动部件在速度变化的上沿(正阶跃)或下沿(负阶跃)存在一个特定的过渡过程,这个过渡过程即是激励持续的时间。

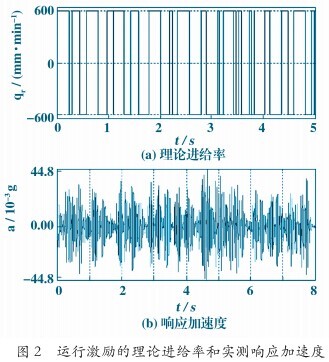
在一台中型数控机床上以单轴进给运动激励机床结构,为了提高激励力的幅值和能量,采用原地往复启停运动方式进给,每个启停运动以伪随机序列出现,理论进给率qr变化如图2(a)所示。
使用LMS SCADAS Mobile数据前端和PCB公司的356A16型ICP三向加速度传感器测试结构上的响应加速度。通过分析不同qr和加减速度时间常数作用下的振动响应,确定激励运动的加减速度时间常数为16ms,qr=600mm/min。图2(b)为该参数条件下测得结构响应加速度幅值。
使用随机减量法(RDT)从振动响应信号中提取自由响应信号,结合ITD法识别机床结构的模态参数。
得到一系列子样本响应x(t-ti),式中:D(t)是初始位移为1mm且初始速度为0mm/s的系统自由振动响应;v(t)是初始位移为0mm且初始速度为1mm/s的系统自由振动响应;x(0)和x(0)分别是系统在t=0时刻的初始位移和初始速度;h(t)是系统单位脉冲响应函数;f(t)是外部激励力;τ为积分时间变量。
将子样本序列的时间起点ti移到坐标原点,通过无偏估计得到初始位移为A,初始速度为0m/s的自由振动响应E[x(t)]≈AD(t)。

以RDT提取自由响应信号时,输出数据的长度L会影响识别结果的精度,ITD法中识别模态数N 取值不当,识别结果也会有较大误差。L和N的取值决定应用RDT和ITD法所得识别结果的准确性。
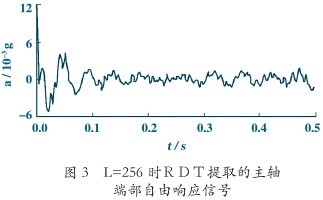
主轴端部的频率和阻尼比直接影响到加工;因此,使用RDT结合ITD方法识别主轴端部的动态特性参数。RDT输出数据长度L过小,会影响ITD法识别结果的精度;L取值过大,输出数据中的过多噪音信号将淹没真实信号,分别以L=128,256,384,512提取主轴端部的响应信号,经过对比最终确定以L=256的提取结果作为ITD法识别模态参数的输入信号,如图3所示。
为了最终得到结构的真实模态,通过以下方法去除伪模态。
a.在ITD识别结果中,先去除其中的非共轭根和重复根。
b.工程经验认为实际结构的阻尼比ζ一般不超过20%,以此作为判据。
c.由模态稳定性原理知伪模态的识别参数对不同阶次敏感异变,故对非稳定模态进行去除。最后,识别结果中出现最多、逐渐趋于稳定的模态参数则为系统的真实模态。
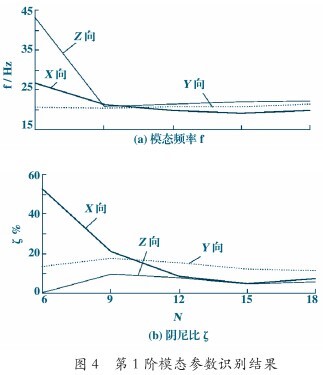
以a和b对每次N值的识别结果进行预处理,通过c综合观察各次识别结果,可得到结构的真实模态参数。图4是第1阶模态频率f和阻尼比ζ的过程数据.从图中可以看出:当N=6时,在机床坐标系Z向上识别出的f偏差较大,X向上识别出的ζ严重偏离合理的值范围。不断提高N值,该阶模态的f和ζ迅速趋于稳定。当N=18时,机床坐标系3个方向上识别出的f和ζ已达稳定。表1中列出了3个方向上,根据本文所提方法识别出的主轴端部3阶模态的f和ζ值。

在该中型数控机床上进行锤激法实验模态分析,力锤量程120kN,灵敏度4.31pc/N。锤头选用尼龙材料,以保证激励能量集中在中低频范围内.实验模态分析结果见表2。
从表1和表2中数据可以看出:与实验模态分析方法得到结果相比,本文所提出方法的第1阶模态频率的绝对误差不超过2.5Hz;第2和3阶模态频率的相对差不超过5%。总体绝对误差除X向上的第2阶误差较大外,其余绝对误差接近或低于2Hz。2种方法都反映出相同的变化规律,即机床结构在Y 向和Z向上的第1阶模态频率基本一致,略大于X 向的模态频率。第2和3阶模态频率在3个方向基本相同。
数控机床运行激励实验模态分析方法,以数控机床自身运动实现结构振动激励,可用于传统激励手段难以甚至无法有效实施的大型重型数控机床的结构动态特性分析。在今后的工作中,需要通过改进模态参数识别方法,并深入研究机床在静止和运动条件下的边界条件和阻尼特性差异,进一步提高本方法的阻尼比识别精度。
 销售热线:159 8941 5020
销售热线:159 8941 5020