基于ANSYS Workbench的数控车床主轴系统热结构耦合分析
0 引言
3 机床热源及边界条件计算
式中,Re为雷诺数,Pr为普朗特数。
式中,C、n为常数由相关参考文献查出;Gr为格拉晓夫准数;g为重力加速度;β为体膨胀系数:L为形状特征尺寸;v为运动粘度;ΔT为流体与壁面温差。
4 主轴系统热特性有限元分析
本文研究以主轴n=3000r/min机床最高工作转速为计算依据,空转3小时达到热平衡状态,根据前述计算公式,可以得到前轴承(靠近刀具端)发热量为56.145W,后轴承(远离刀具端)发热量为48.73W;主轴内表面传热系数为213.667W/m2℃ 主轴外表面的传热系数为107.189W/m2℃,床头箱内其他表面传热系数为9W/m2℃。将以上边界条件约束到有限元模型上,得到主轴系统的温度场分布如图3。
由上图可知,主轴最高温度发生在主轴前端轴承安装处达52.09℃,后端轴承安装处温度达48.15℃,箱体温度较低且温度分布不均匀,前后轴承温升不一致,最大温升为32℃(空气温度假设为20℃情况下),从温度场分布可知由于在轴承安装处温升不同将导致主轴系统发生一定的热膨胀,从而产生热变形。
为了验证模型计算的正确性,采用非接触式红外温度测量仪对主轴系统作了温度测试实验分析,具体操作如下:在n=3000r/min,机床正常空转3小时后,测温点分布在主轴前后端轴承附近,取主轴圆周等分位置四点多次测量取平均值,同时还测量了箱体表面的温度。实验得到前端轴承附近温度测量值为48.9℃,理论分析值误差为6.5%;后端轴承附近温度测量值为46.5℃,理论分析值误差为3.5%;箱体侧表面温度测量值为43.1℃理论分析值误差为5.6%。由以上分析得到的结果误差基本上控制在7%以内,可以认为由模型得到的计算结果是可靠的,与实际情况相符。
由上图可知,机床主轴系统最大变形发生在床头箱体底部一小范围,达54.537μm,主轴系统主轴前端径向位移为8.9μm、综合位移为30.298μm;主轴后端径向位移为12.2μm,综合位移为42.417μm,有一定的变形,但还是符合加工精度要求。
机床的热特性问题一直阻碍加工精度的进一步提高,热控制技术是研制高精度机床工作中急需解决的关键技术之一。由于机床在正常工作条件下,热源(电机、轴承等)产生的热量传给机床部件,使各部位产生一定的温升,同时零部件产生热变形。由于零件结构、形状等尺寸不一,将产生弯曲、扭曲、拉伸等变形即热位移,这样造成主轴、工作台、刀具等部位发生一定的相对位移,从而影响加工精度,使加工精度大大降低。机床主轴等重要零部件热变形误差是引起机床变形误差的重要因素,因此在机床设计时,减少主轴系统的发热和加强散热,降低温升,通过对主轴系统进行热特性分析是保证机床的加工精度的重要措施。
采用有限元数值分析软件可以较好地分析这个问题。ANSYS Workbench 12是ANSYS求解实际问题的新一代产品。除了可以解决静力学、动力学、非线性接触分析以外还支持直接耦合场分析、如热-结构、热-电、热-磁耦合等。热-结构耦合分析是耦合物理场分析中比较常见和重要的一种,本文以柳州市数控机床研究所研发的CK6136数控车床主轴系统为研究对象,建立主轴系统热特性分析的有限元模型,在有限元分析软件ANSYS Workbench 12中对其进行热稳态分析,到主轴的温升和温度场分布情况,以求得的温度场为依据进行热-结构耦合分析计算得到其热变形,同时计算主轴不同转速条件下对主轴系统产生的温升及热变形的影响,最后得出相关结论。
1 热分析基本理论
对于稳定热分析,如果系统的净热流率为0,即流入系统的热量加上系统自身产生的热量等于流出系统的热量:q流入+ q生成- q流出= 0,在稳态热分析中任一节点的温度不随时间变化。稳态热分析的能量平衡方程为:
式(1)中:
[K]为传导矩阵,包含导热系数,对流系数及辐射率和形状系数;
{T}为节点温度向量;
{Q}为节点热流率向量,包含热生成。
根据参考文献,由边界条件和载荷结合热应力分析可以推导出整体刚度矩阵[K]和载荷向量{P}:
式(2)、式(3)中[K]e为单元刚度矩阵,{P}e为单元节点载荷,{P}eT为单元节点热载荷。
根据位移模式,由平衡条件、变分原理及胡克定律[K]·{δ}={P}可以推导出节点位移{δ},由单元节点位移{δ}eT及温升{ΔT}e,计算获得总应变{ε}及热变形{ε}T,最终热应力表达式为:
式(4)中[D]为弹性矩阵。
2 主轴系统有限元模型
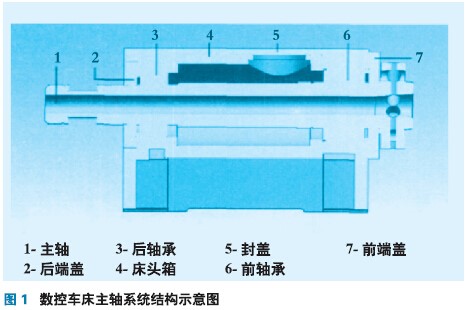
本文研究对象CK6136 数控车床主轴系统主要由主轴、前后角接触球轴承、床头箱、封盖前后端盖等部件组成,对于复杂结构在进行CAD建模时需要对模型进行适当的简化。例如模型中的圆角和倒角以及对分析结果不造成很大影响的小孔就应该尽量省略,还有将键槽、螺纹孔、挡油孔均按实体处理等,在三维软件UG6.0建立好主轴系统结构简图(半剖视图)如图1所示,同时设置好UG6.0和ANSYS Workbench 12的无缝连接。
3.1 热源分析
对于数控车床主轴系统热源分析本文主要考虑前、后轴承的摩擦发热,而忽略电动机发热、切削热发热对主轴系统的影响,根据参考文献主轴轴承热源的计算公式如下:
式(5)中M为轴承摩擦力矩,指由轴承滚动摩擦、滑动摩擦和润滑剂摩擦的总和产生的阻滞轴承运转的阻力矩;n为轴承转速。M的计算公式如下:
式(6)中M1为和轴承载荷大小、滚动体和滚道间接触弹性变形量及滑动摩擦有关的摩擦力矩分量,M1的计算公式如下:
M2为与速度有关的选项,它反映润滑剂的流体动力消耗,M2的计算公式如下:
(1)当vn>3. 33×10-5m2·r /s2 时:
(1)当vn< 3. 33×10-5m2·r /s2 时:
上式(7)~式(9)中,f1为轴承类型和所受负荷有关的系数;p1为轴承摩擦力矩的计算负荷,f1和p1可查阅相关资料查得;f0为与轴承类型和润滑方式有关的常数;v为润滑剂的运动粘度;dm为轴承中径;n为轴承转速。
3.2 换热系数的计算
在空转且不考虑冷却液的条件下主轴部件对流则是主轴部件表面与空气之间的对流,根据参考文献由努谢尔特准则,换热系数计算公式为:

(1)对于主轴
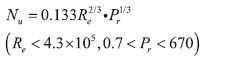
(2)对于床头箱
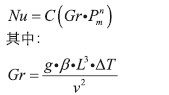
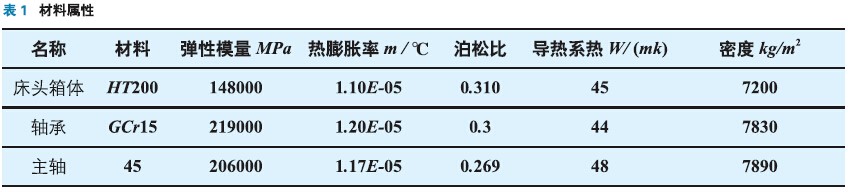
3.3 材料属性设置
在ANSYS Workbench 12中重新添加床头箱,轴承和主轴三种材料,其材料属性见表1。
4.1 热稳态分析
将模型导人有限元分析软件ANSYS Workbench 12中,对主轴系统模型进行四面体网格划分,网格划分后得到1807105个节点,1184866个单元,网格划分模型如图2所示。


4.2 热-结构耦合分析
在有限元分析软件ANSYS Workbench12中利用直接耦合顺序耦合解方法,将得到的温度场的温度分布作为热载荷加载到模型上,同时约束床头箱体底部与床身接触面的所有自由度,计算得到主轴系统的热变形如图4所示。

4.3 主轴转速变化对主轴系统温升及热变形的影响
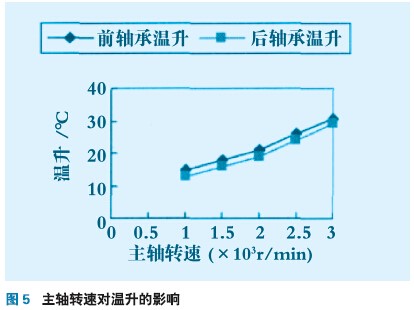
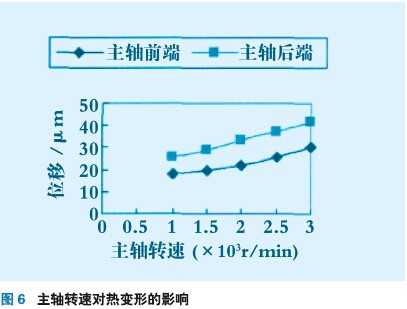
由式(5)~式(9),计算出不同主轴转速条件下前后轴承的发热量见表2。在有限元分析软件中重新计算得到主轴转速变化对主轴系统产生的温升及热变形的影响如图5、图6所示。

5 结束语
本文通过有限元分析软件ANSYS Workbench12对数控车床主轴系统进行热特性分析,求得该系统的温度场分布、温升、和热变形,得到主轴不同转速条件对主轴系统温升及热变形的影响,并且通过温度测量实验验证了有限元模型计算的正确性,计算的结果基本符合要求。具体结论如下:
(1)通过有限元分析软件对主轴系统进行热特性分析,是一种简单可靠的方法;
(2)通过对主轴系统的热-结构耦合分析可知主轴轴承发热量较大,产生较大温升,最高温升发生在前端轴承安装处,温度变化将导致机床产生一定的热变形,对加工精度有一定的影响,可通过改变润滑油、冷却条件、误差补偿等降低轴承温升,减少变形量;
(3)通过有限元分析可知,主轴转速越高,相应的轴承发热量越高,由此产生的温升变化对主轴的热变形也越高,这与实际情况是相符的。
 销售热线:159 8941 5020
销售热线:159 8941 5020