基于分段拟合的机床大尺寸工作台热误差补偿模型
0 前言
在影响零件加工精度的因素中,机床热误差是影响加工精度的主要原因之一,在精密机床加工中由于热因素造成的加工误差可以占到60% ~70%。为降低或消除机床热误差对加工精度的影响,科研人员进行了大量广泛深入的研究,目前主要有两种减小热误差的途径:硬件消除法和软件补偿法。硬件消除法主要是通过热结构对称设计、预拉伸和采用低热膨胀系数的材料来实现,硬件消除法缺点是成本较高。软件补偿法是通过建立能够反映机床温度与热误差关系的数学模型,在补偿时用模型产生的预测值来抵消机床因温度变化产生的误差,以此达到消除热误差的目的。软件补偿法的优点是,实现成本较低且无须对现有机床进行大的改造,应用简便易于推广。软件补偿法的关键是建立能够准确反映机床温度与误差之间的数学模型,这也是目前热误差补偿研究工作的热点和难点。补偿模型分为离线静态模型和在线动态实时模型,常见静态补偿模型如:多元统计回归、最小二乘支持向量机、灰色系统理论、神经网络等。如果机床使用环境和建模环境相近,静态热误差模型能够取得较好的预测效果,但是当机床使用环境和建模环境相差比较大或环境温度和工况变化比较大时,模型预测精度会严重受到影响。为了提高热误差补偿模型的精度和适应能力,研究者提出了实时在线动态补偿模型,在线模型能够根据加工状况、环境温度等的变化实时调整模型参数,使模型能跟踪机床热误差的变化,所以在线动态模型具有更高的预测精度和适应能力。
以上建模方法为热误差补偿提供了有力工具,且在试验中取得了良好效果。机床部件受热不仅会产生热膨胀伸长,还会产生弯曲变形。如丝杠螺母在传动过程中由于摩擦作用产生热,文献分析了丝杠热弹性效应导致对工作台纵向定位精度的影响。文献提出一种几何误差和热误差建模方法,对热误差分离后,建立了不同位置不同温度下的热误差补偿模型,提高了工作台定位精度。实际工作中丝杠螺母摩擦热一部分传入丝杠,还有一部分传入工作台,传入工作台的这部分热,分布不均匀将会导致工作台热变形。现有文献在热误差建模时对工作台热变形考虑较少,本文在三坐标铣床上通过试验发现丝杠螺母传入工作台的热导致工作台两侧产生翘曲,为了对工作台热变形造成的热误差进行补偿,先建立工作台不同位置热误差模型,再对工作台各点模型预测值进行分段拟合,实现对工作台任意位置的热误差预测。为了增加模型的预测精度和适应能力,通过聚类分析和逐步回归寻找最佳测温点,采用粒子群优化实时辨识动态模型参数,提高了模型鲁棒性和预测精度。
1 温度测点的选取及建模方法
在选取温度测点时认为不同位置温度点只要温度变化规律相似,对热误差模型的作用就相似,在建模时可以从相似的测点中选取一个作为代表变量,机床热误差模型可以用几个关键的温度点来表征。基于上述假设,可以在机床上布置大量传感器,然后根据每点的温度变化规律进行分类,再从每个分类中选取一个温度变量进行热误差建模。这样就减小了温度测点选取的盲目性,且能利用较少的温度变量建立热误差模型。本研究先用聚类分析方法对温度变量进行分类,再利用逐步回归选取与热误差变化最相关的温度测点,然后根据选取的测点作为输入变量,建立差分热误差模型。
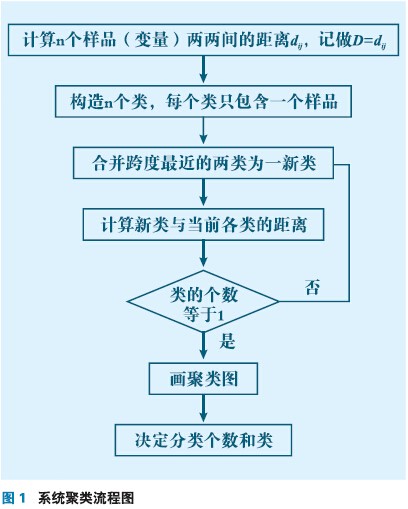
(1)聚类分析方法。聚类分析是一种分类方法,它能将一批样品或变量,按照它们在某种评定标准上的相似程度或远近进行分类,目的是使同类内对象的同质性最大和类与类之间的对象差异性最大。为了对样品(变量)进行分类,一般采用两种方法:①相似系数法,性质越相似或越接近的它们相似系数为1,彼此无关的相似系数接近0,相似的样品(变量)归为一类;② 距离法,把样品看做空间中的一个点,然后定义距离,距离近的点归为一类。常用的分类方法有5种:即最短距离法、最长距离法、类平均法、重心法、离差平方和法。
这5种聚类法的计算步骤一样,不同的是距离的定义方法,当采用欧氏距离时5种方法有统一的递推公式中,
Dkr表示类Gk与类Gr之间的距离,
(2)逐步回归原理。逐步回归原理是在建立因变量和自变量回归模型时,自变量逐次引入,每引入一个自变量,对进入的变量进行逐个检验,当原引入的变量由于后面变量的进入而变得不再显著时,就将其剔除。引入或剔除一个变量称为逐步回归的一步,每步都要进行F 检验,以确保新引入变量前,回归方程中只包含显著地变量。这个过程反复进行,直到既无新的变量进入回归方程也无变量可剔除,计算停止得到逐步回归下的最优方程。
1.2 建模原理
(1)差分方程模型。差分方程输出值不仅与当前的输入值有关还和历史输入有关,而热误差的变化也与历史热输入大小有关,因此采用差分结构描述热膨胀更符合其物理意义。差分方程建模属于动态建模,差分方程形式如式(2)所示
式中,
(2)模型参数实时辨识方法。采用粒子群优化算法,根据实时反馈的温度和热误差数据对模型参数进行辨识。
基于粒子群优化算法辨识原理:粒子群优化算法(Particle swarm optimization, PSO)是一种群体优化算法,来源于人工生命和演化计算理论。基本原理如下:求解问题时,每个粒子都随机设置初始位置和初始速度,初始位置表示在解空间中的一组解,速度表示搜索解空间的快慢。如在D 维空间中搜索,每个粒子就可以用D 维矢量表示,第i 个粒子的位置表示为x=(xi1,xi2,…,xiD),速度表示为vi= (vi1,vi2,…,viD)。每个粒子适应度的优劣由适应度函数F 评价,粒子经过一次迭代,搜索到的个体最优值: pi= (pi1,pi2,…,piD),群体最优值:pg = (pg1,pg2,…,pgD),然后再跟据式(3)更新粒子位置和速度
式中,
式中,y0(t)为实际系统输出;
2 热误差试验
2.1 试验安排
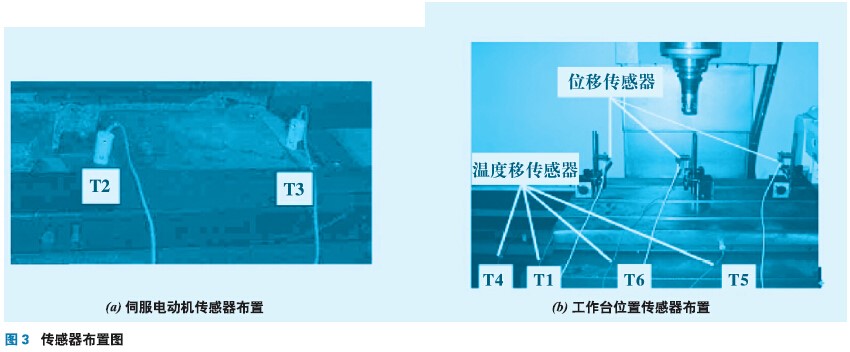
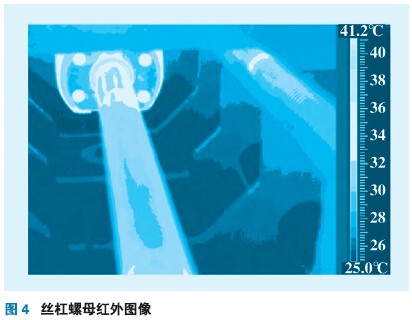
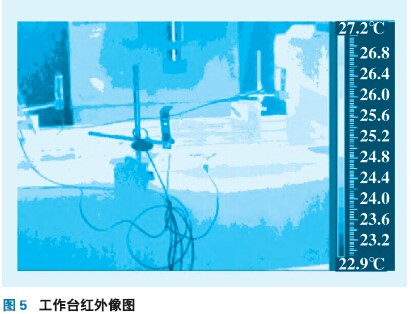
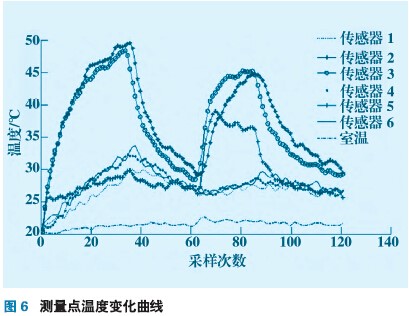
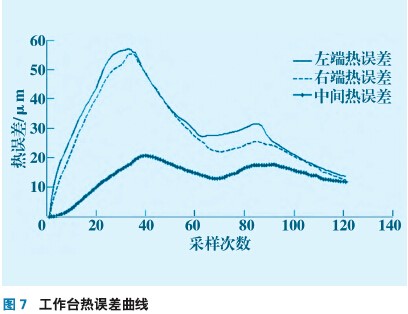
本试验以三坐标铣床工作台为研究对象,x 轴以指令G00快速移动时,测量在工作台长度方向最左、中、最右三个点纵向热变形(工作台尺寸:长900 mm,宽410 mm)。传感器安装如图3所示,T1放置在丝杠螺母附近;T2,T3 放置在伺服电机减速器上;T4放置在丝杠轴承座上;T5,T6放置在工作台中间;T7测量环境温度。电涡流位移传感器分别安装在工作台最左、中、最右三个位置。工作台x轴行程0~500 mm;往复移动速度(以指令G00快速运行);第一个升温阶段快速运行2.5h,停止2.5h;第二个升温阶段运行(第一阶段速度的70%)2.5h,停止2.5 h;每隔5 min 对测点温度和热误差进行一次采样。工作台运行1h后的丝杠螺母和工作台的红外图像如图4、5所示;温度和热误差测量数据如图6、7 所示。
图4、5 表明,工作台运动时丝杠螺母处温度比较高,局部可以达到40℃,由此传入工作台使工作台表面中间部位温度高,两侧温度低,工作台上表面最高温度27 ℃,说明从丝杠螺母处到工作台上表面存在温度梯度。
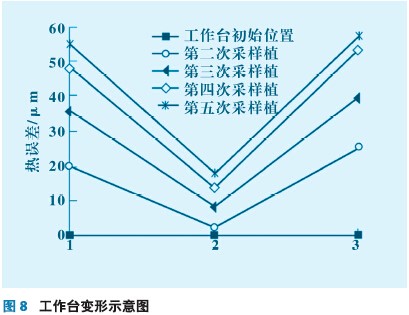
试验测量的温度和热误差曲线图6、7所示。从图6和图7看出,当测点温度随机床工作状态变化时,工作台纵向误差也随之发生改变,而且工作台两侧和中间热误差变形量不同,也就是说工作台热变形后呈“凹状”。根据这一现象,对机床纵向加工误差进行补偿时,不能采取固定值,而应该随着工作台的位置不同而采取不同的补偿量使之适应工作台面随温度和位置的变化。整个工作台随着受热变形规律及变形量可由图8表示。从图8中看出工作台在热变形时,两侧的热变形量要大于中间的热膨胀量且两侧变形速度大于中间位置,导致工作台两侧翘曲,使台面呈凹状。
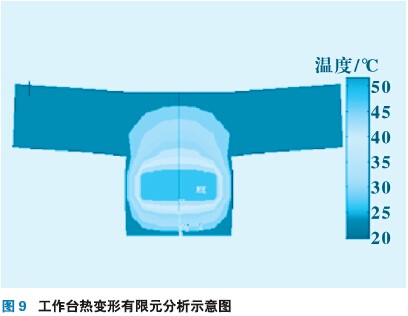
为了验证工作台在连续往复工作时由于热变形呈“凹状”这一现象是否符合物理原理,采用有限元法进行验证(由于有限元仿真边界条件不可能完全符合实际工作条件,仿真数据可能和实测数据有差异,但是结果能够反映该变化的趋势,所以可以利用有限元法进行验证这种现象),如图9所示。有限元热变形图是在丝杠螺母处给定摄氏温度60 ℃,仿真时间为20min的结果。从图9上能明显看出工作台两侧发生翘曲,与试验结果得到的现象相吻合,说明试验观察到的现象是可能发生的。
3 温度测点选取及热误差建模
3.1 最佳温度测点的选取
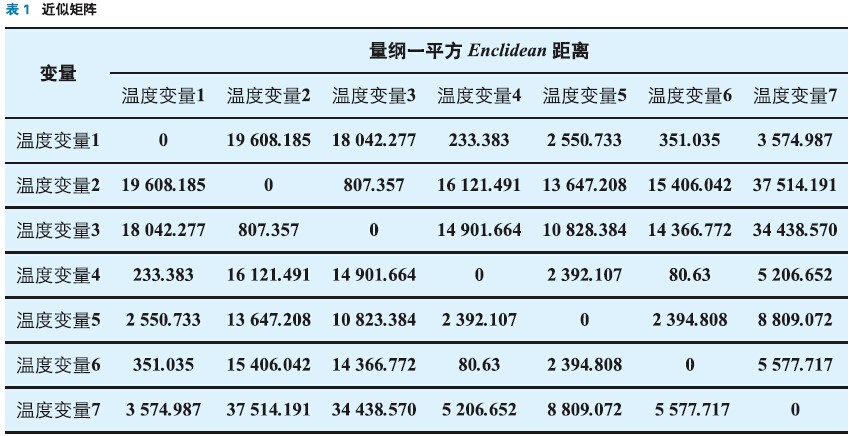
对7个温度变量进行系统聚类分析,采用最短距离法,平方Euclidean距离,计算出两两变量的近似矩阵,如表1所示。
根据计算的近似系数,按图1流程得到图10所示聚类树,纵坐标是变量个数,横坐标聚合指数是将实际的距离按照比例调整到0~25的范围内。7个温度变量按照四类进行选取,从每一类中选取一个变量得到T1、T5、T7、T2四个为基本待选变量。
方程复相关系数R = 87%,各变量因子显著水平远小于0.05,说明各自变量与因变量线性相关程度显著,由此选取和热误差有显著关系的温度变量为T1和T2。
3.2 差分方程阶次的确定
确定方程阶次是采用从1 阶逐次递增,同时考察模型预测值与测量值残差平方和的大小来确定,当增加阶次残差平方和变化不明显时,采用此时阶次值。根据上面方法并考虑运算简单性,确定差分方程为二阶
由于工作台两侧和中间的变形量不一样,因此需要3个模型分别对工作台左侧、中间和右侧热误差进行预测。如果工作台左右两侧热误差相差很小,可以共用1个模型进行预测。
3.3 参数模型实时辨识
确定热误差模型结构后,采用粒子群优化算法对模型参数进行辨识。对热误差模型参数辨识并不是每个反馈周期都进行,而是当模型输出值和热误差反馈值残差超过一定范围时,再启动辨识算法对模型参数进行辨识更新。辨识的输入数据为最近的10次采样数据,使热误差模型始终反映机床最新的工作状态。
3.4 拟合模型的建立
设EL(t),EM(t),ER(t)分别为工作台左侧、中间和右侧在t 时刻的热误差模型预测值,为对工作台左半部分行热误差预测,利用EL(t)和EM(t)进行直线拟合得到拟合公式(6),由于不同时刻EL(t)和EM(t)取值不同,所以a和b是时变系数
式中,
4 热误差建模结果及分析
4.1 单点模型建模结果及分析
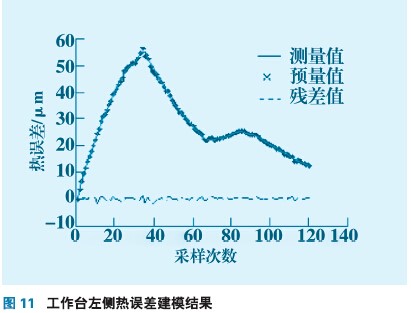
由于工作台中间热误差模型和两侧热误差模型结构形式相同,辨识算法也一样,在此只给出工作台左侧热误差模型验证结果。采用粒子群优化参数辨识工作台左侧模型参数,辨识结果如图11所示。
通过图11看出,在第一个升温阶段模型预测值与测量值符合较好残差很小,因为此阶段工况单一,热误差模型能够进行较好的预测;当温度开始下降时,在第38个采样时刻出现一次波动,说明热误差模型参数和机床状态不匹配,残差超出限定值需要更新模型参数,更新模型参数后直到下一个升温过程,预测值效果良好,残差值较小。在第68个采样时刻残差又出现一次波动,模型进行参数更新,使热误差模型随着机床热状态的变化而实时调整。说明该算法有一定的自适应能力,能够根据残差的变化实时更新模型参数,模型预测结果如表2所示。
4.2 分段拟合模型验证及分析
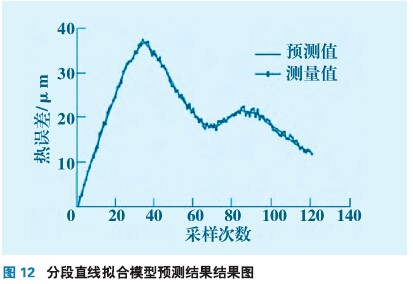
通过上述辨识过程得到工作台中间和两侧的单点热误差模型,要对工作台整体范围进行热误差补偿,还需要进一步对热误差模型进行扩展,因为上述热误差模型只是描述工作台三个位置的热误差状态。为了对整个台面的热误差进行补偿,对每一时刻预测值得到的左、中和右三个数值进行分段拟合得到拟合公式,在补偿时由分段拟合公式得到工作台任意位置的热误差量,这样就可以做到对整个工作台的任意位置进行补偿。为验证这一过程,在工作台中间传感器和最左端传感器中间处再放置一个位移传感器,用来测量该位置的热误差值作为验证值。预测模型采用最左端和中间热误差模型的预测值做直线拟合,然后根据得到的直线模型对中间点进行预测。直线分段拟合模型预测值与测量值进行比较,结果如图12所示,残差指标如表3所示。
从图12和表3看出,采用两点直线拟合公式对中间热进行预测,效果良好,采用直线分段拟合方法能够实现对工作台任意位置的纵向热误差精确预测。根据此原理很容易建立工作台右侧部分的直线分段拟合模型。
5 结论
1.1 温度测点的选取方法
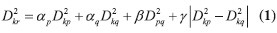
Gr是Gq和Gp合并后形成的新类。
αp,αq, β, γ对不同方法有不同的取值,具体取值参见文献。采用系统聚类法进行分类的流程如图1所示。
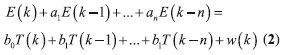
k 表示采样时刻;
a, b 为方程系数;
n 为差分方程的阶次;
E(k), T(K)分别为系统的输出和输入序列。
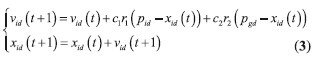
i=1,2,…,N;
d=1,2,…,D;
c1 和c2是非负常数;
r1和r2是介于[0,1]的随机数;
vid ∈[vmax,vmax ], vmax为粒子最大速度;
t为当前迭代次数。
PSO算法流程图如图2所示。PSO算法进行系统辨识,可以看成是一优化过程,适应度函数取如下
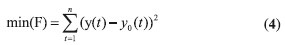

y(t)为模型输出,min为取适应度函数的最小值。
PSO 算法进行系统辨识是使一组粒子作为模型参数,使式(4)取得最小值,对应的这组粒子就是待求模型参数。
2.2 试验结果定性分析

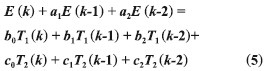

x为工作台位置,
a、b为线性方程系数。
利用式(6)可以对工作台左侧部分,进行任意位置的纵向热误差预测。同理可以建立工作台右侧部分的线性预测模型。


(2)通过粒子群优化算法,能够根据反馈数据对二阶差分模型参数进行实时辨识,使模型能够跟踪机床热误差的变化,从而使模型保持较高的预测精度。
(3)试验中发现机床工作台两侧翘曲现象,通过对铣床工作台x方向左、中、右三点分别建立热误差模型,再通过对三点热误差模型各时刻预测值进行分段拟合,实现对工作台任意位置热误差补偿。为了对更大尺寸工作台进行热误差补偿,只需要按照此原理在工作台上布置更多的热误差传感器,建立对应点的热误差模型,然后对各模型预测值进行分段拟合得到整个工作台的纵向热误差补偿模型。为了进一步提高多点模型拟合的精度,可以采用高次多项进行多点拟合。该方法为大尺寸工作台纵向热误差补偿提供了一种新思路。
 销售热线:159 8941 5020
销售热线:159 8941 5020